The overall goal of this series of write-ups is to explore a number of models performing binary classification on a given set of images. This is the second write-up in the series where we advance from utilizing a logistic regression model with gradient descent to a shallow neural network. Our hope is that for each of the write-ups we’ll advance to utilizing a more sophisticated model and achieve better and better classification results.
The model created in this write-up be to perform binary classification on a set of images utilizing a shallow neural network, predict (hopefully correctly) if a given image is a cat or not (hence the binary nature of the model), and if possible to perform the classification task better than the previously developed system.
Comparisons between the models will be achieved through accuracy ratings on the test set, as well as the model’s F-Score.
For reference here are links to the previous entries in this series:
So, let’s get started!
Notes on the How this Write-up Evolved
When I first started this write-up I was mostly focused on the mechanics of building the model. I spend about an hour writing the code, and then fed in my data set. The accuracy was poor and the cost function didn’t monotonically decrease along with other issues. I adjusted, adjusted, and then adjusted the model some more, and its performance still fell short or barely exceeded what the previous logistic regression model was able to achieve.
And so, at that time, the real focus of this write-up become apparent: The mechanics of building the model were easy, it was the TUNING of the model that was would require the real effort.
And so that realization is what fueled most of the work done during this write-up. I needed a way to quickly generate and adjust all the hyperparameters which previously I didn’t have to contend with, record the results, and then compare the outputs to select the best model.
This in turn required I modify the model’s code, write a better model execution utility, deal with how to display the outputs of multiple models, manage the display of many cost graphs, and so on and so forth. So below are the fruits of those efforts, and as we continue to delve into additional models and optimizations I have no doubts we’ll continue to evolve our utility set.
Model Code Development
Import libraries and data sets
%matplotlib inline
# autoreload reloads modules automatically before entering the execution of code typed at the IPython prompt.
%load_ext autoreload
%autoreload 2
import warnings
warnings.filterwarnings('ignore')
from os import path
from utils import *
import pandas as pd
from IPython.display import display, HTML
import numpy as np
from matplotlib import pyplot as plt
import inspect
import time
import copy
import random
random.seed(10)
np.random.seed(10)
# Examine the data used for training the model
imageData = path.join("datasets", "imageData500_64pixels.hdf5")
validateArchive(imageData)
*** KEYS
HDF5 container keys: ['testData', 'testLabels', 'trainData', 'trainLabels']
*** LABELS
Total number of training labels: 800
Number of cat labels: 396
Number of object labels: 404
First 10 training labels: [0 0 1 1 1 1 1 1 0]
Total number of testing labels: 200
Number of cat labels: 104
Number of object labels: 96
First 10 testing labels: [1 1 0 0 1 1 0 0 0]
*** IMAGE DATA
Image data shape in archive: (800, 64, 64, 3)
First HDF5 container dataSet item shape: (64, 64, 3)
Image data shape after flattening: (192, 64)
First 10 dataSet item matrix values: []
Recreating and showing first 20 images from flattened matrix values:




# Load, shape, and normalize the data used for training the model
with h5py.File(imageData, "r") as archive:
trainingData = np.squeeze(archive["trainData"][:])
testData = np.squeeze(archive["testData"][:])
trainingLabels = np.array(archive["trainLabels"][:])
testLabels = np.array(archive["testLabels"][:])
archive.close()
print("Archive trainingData.shape: ", trainingData.shape)
print("Archive trainingLabels.shape: ", trainingLabels.shape)
print("Archive testData.shape: ", testData.shape)
print("Archive testLabels.shape: ", testLabels.shape)
print("\n")
# Reshape the training and test data and label matrices
trainingData = trainingData.reshape(trainingData.shape[0], -1).T
testData = testData.reshape(testData.shape[0], -1).T
print ("Flattened, normalized trainingData shape: " + str(trainingData.shape))
print ("Flattened, normalized testData shape: " + str(testData.shape))
# Normalization
trainingData = trainingData/255.
testData = testData/255.
Archive trainingData.shape: (800, 64, 64, 3)
Archive trainingLabels.shape: (1, 800)
Archive testData.shape: (200, 64, 64, 3)
Archive testLabels.shape: (1, 200)
Flattened, normalized trainingData shape: (12288, 800)
Flattened, normalized testData shape: (12288, 200)
Write utility functions
# Great reference: https://www.python-course.eu/matplotlib_multiple_figures.php
# Write a function to show multiple graphs in the same figure
def printCostGraphs(costs, keys, cols, fsize = (15,6)):
# Figure out how many rows and columns we need
counter = 0
rows = np.ceil(len(costs) / cols)
fig = plt.figure(figsize = fsize)
# Add each of the cost graphs to the figure
for key in keys:
c = np.squeeze(costs[key])
sub = fig.add_subplot(rows, cols, counter + 1)
sub.set_title('Epoch ' + str(key))
sub.plot(c)
counter = counter + 1
# Draw the figure on the page
plt.plot()
plt.tight_layout()
plt.show()
# Randomize values for hyperparameters based on a given key:value dictionary
class HPicker:
def pick(self, ranges):
hParams = {}
# For each parameter key:val
for key, value in ranges.items():
if isinstance(value, list):
start, stop, step = value
vals = []
# Create a range of possible values
while (start < stop):
start = round(start + step, len(str(step)))
vals.append(start)
# Pick one of the possible values randomly
hParams[key] = random.choice(vals)
else:
hParams[key] = value
return hParams
# Create instances of each of the activations we might utilize in the model
class AbstractActivation(object):
def activate(self, z):
raise NotImplementedError("Requires implementation by inheriting class.")
class Sigmoid(AbstractActivation):
def activate(z):
return 1 / (1 + np.exp(-(z)))
class Relu(AbstractActivation):
def activate(z):
return z * (z > 0)
# Create a pandas dataframe with labeled columns to record model training results
def getResultsDF(hRanges):
columns = list(hRanges.keys())
df = pd.DataFrame(columns = columns)
return(df)
# Do all the heavy lifting required when running N number of models with various hyperparameter configurations
def runModels(hRanges, epochs, silent = False):
# Var inits
picker = HPicker()
resultsDF = getResultsDF(hRanges)
costs = {}
params = {}
epoch = 0
print("\n*** Starting model training")
while (epoch < epochs):
# Get the random hyperparam values
hparams = picker.pick(hRanges)
hparams["Epoch"] = epoch
# Print a summary of the model about to be trained and its params to the user
if silent is not True:
print("Training epoch", epoch, "with params: LR", hparams["Learning_Rate"],
", iterations", hparams["Iterations"], ", HL units", hparams["HL_Units"],
", lambda", hparams["Lambda"], ", and init. multi.", hparams["Weight_Multi"])
# Train the model its given hyperparams and record the results
params[epoch], costs[epoch], hparams["Descending_Graph"] = model(
trainingData, trainingLabels, hparams["HL_Units"], hparams["Iterations"],
hparams["Learning_Rate"], hparams["Lambda"], hparams["Weight_Multi"], False)
# Make predictions based on the model
trainingPreds = predict(trainingData, params[epoch], trainingLabels)
testPreds = predict(testData, params[epoch], testLabels)
# Record prediction results
hparams["Train_Acc"] = trainingPreds["accuracy"]
hparams["Test_Acc"] = testPreds["accuracy"]
hparams["Final_Cost"] = costs[epoch][-1]
# Add model results to the pandas dataframe
resultsDF.loc[epoch] = list(hparams.values())
epoch = epoch + 1
print("*** Done!\n")
# Sort the dataframe so it's easier to find the results we are interested in
resultsDF = resultsDF.sort_values(by = ['Descending_Graph', 'Test_Acc'], ascending = False)
return resultsDF, params, costs
Write the shallow neural network model code
# Define the dimensions of the model
defineDimensions(data, labels, layerSize):
nnDims = {}
nnDims["numberInputs"] = data.shape[0]
nnDims["hiddenLayerSize"] = layerSize
nnDims["numberOutputs"] = labels.shape[0]
return nnDims;
# Initialize model params (i.e. W and b)
def initilizeParameters(dimensionDict, multiplier):
np.random.seed(10) # Yes, this has to be done every time... :(
w1 = np.random.randn(dimensionDict["hiddenLayerSize"], dimensionDict["numberInputs"]) * multiplier
np.random.seed(10) # Yes, this has to be done every time... :(
w2 = np.random.randn(dimensionDict["numberOutputs"], dimensionDict["hiddenLayerSize"]) * multiplier
b1 = np.zeros((dimensionDict["hiddenLayerSize"], 1))
b2 = np.zeros((dimensionDict["numberOutputs"], 1))
params = {
"w1" : w1,
"w2" : w2,
"b1" : b1,
"b2" : b2}
return params
# Perform forward propogation
def forwardPropagation(data, params, activation = Sigmoid()):
w1 = params["w1"]
b1 = params["b1"]
w2 = params["w2"]
b2 = params["b2"]
z1 = np.dot(w1, data) + b1
a1 = np.tanh(z1)
z2 = np.dot(w2, a1) + b2
a2 = Sigmoid.activate(z2)
# Sanity check the dimensions
assert(a2.shape == (1, data.shape[1]))
cache = {"z1": z1,
"a1": a1,
"z2": z2,
"a2": a2}
return cache
# Calculate the cost of the model (includes L2 regularization)
def calculateCost(labels, params, cache, lamb):
# Define vars to make reading and writing the formulas easier below...
m = labels.shape[1]
a2 = cache["a2"]
w1 = params["w1"]
w2 = params["w2"]
# Perform cost and regularization calculations
crossEntropyCost = (-1/m) * np.sum( labels*np.log(a2) + (1-labels)*np.log(1-a2) )
l2RegularizationCost = (1/m) * (lamb/2) * (np.sum(np.square(w1)) + np.sum(np.square(w2)))
finalCost = crossEntropyCost + l2RegularizationCost
return finalCost
# Perform backward propogation
def backwardPropagation(data, labels, params, cache, lamb):
# Define and populate variables
m = data.shape[1]
w1 = params["w1"]
w2 = params["w2"]
a1 = cache["a1"]
a2 = cache["a2"]
# Calculate gradients
dz2 = a2 - labels
dw2 = (1/m) * np.dot(dz2, a1.T) + (lamb/m) * w2
db2 = (1/m) * np.sum(dz2, axis = 1, keepdims = True)
dz1 = np.dot(w2.T, dz2) * (1 - np.power(a1, 2))
dw1 = (1/m) * np.dot(dz1, data.T) + (lamb/m) * w1
db1 = (1/m) * np.sum(dz1, axis = 1, keepdims = True)
# Store in the gradients cache
gradients = {"dw1": dw1,
"db1": db1,
"dw2": dw2,
"db2": db2}
return gradients
# Update the model params based on the results of the backward propogation calculations
def updateParams(params, gradients, learningRate):
params["w1"] = params["w1"] - learningRate * gradients["dw1"]
params["b1"] = params["b1"] - learningRate * gradients["db1"]
params["w2"] = params["w2"] - learningRate * gradients["dw2"]
params["b2"] = params["b2"] - learningRate * gradients["db2"]
return params
# Define the actual neural network classification model
def model(data, labels, layerSize, numIterations, learningRate, lamb, initializeMultiplier, printCost = False, showGraph = False):
# Init vars
dims = defineDimensions(data, labels, layerSize)
params = initilizeParameters(dims, initializeMultiplier)
costs = []
descendingGraph = True
# For each training iteration
for i in range(0, numIterations + 1):
# Forward propagation
cache = forwardPropagation(data, params)
# Cost function
cost = calculateCost(labels, params, cache, lamb)
# Backward propagation
grads = backwardPropagation(data, labels, params, cache, lamb)
# Gradient descent parameter update
params = updateParams(params, grads, learningRate)
# Print the cost every N number of iterations
if printCost and i % 500 == 0:
print ("Cost after iteration", str(i), "is", str(cost))
# Record the cost every N number of iterations
if i % 500 == 0:
if (len(costs) != 0) and (cost > costs[-1]):
descendingGraph = False
costs.append(cost)
# Print the model training cost graph
if showGraph:
_costs = np.squeeze(costs)
plt.plot(_costs)
plt.ylabel('Cost')
plt.xlabel('Iterations (every 100)')
plt.title("Learning rate =" + str(learningRate))
plt.show()
return params, costs, descendingGraph
# Utilize the model's trained params to make predictions
def predict(data, params, trueLabels):
# Apply the training weights and the sigmoid activation to the inputs
cache = forwardPropagation(data, params)
# Classify anything with a probability of greater than 0.5 to a 1 (i.e. cat) classification
predictions = (cache["a2"] > 0.5)
accuracy = 100 - np.mean(np.abs(predictions - trueLabels)) * 100
preds = {"predictions" : predictions, "accuracy": accuracy}
return preds
Model Training with Variable Hyperparameters
It’s finally time to test the model with a number of hyperparameter configurations, and we’ll see if we can find a combination of hyperparameters that optimizes and improves on the classification prediction rate.
For reference here is what we achieved without model tuning:
Train accuracy: 90.625
Test accuracy: 62.0
We’ll start with 80 models utilizing a smaller learning rate with more and less iterations, and then we’ll take a look at another 80 models having a larger learning rate again with more and less iterations. Hopefully one or more of the 160 models will have good results, and we can then look at its F-Score for comparison to the logistic regression model we generated in the last write-up.
For each model the hyperparameters will be generated randomly from a defined range. This should help us to quickly explore a number of combinations without having to hand-craft each one.
Smaller learning rate training
h1 = {
"Epoch": None,
"HL_Units": [2, 8, 1],
"HL_Size": 1,
"Iterations": [750, 2000, 50],
"Learning_Rate": [0, .01, .001],
"Lambda": [0, 2, .1],
"Weight_Multi": [0, 0.001, .0001],
"Train_Acc": None,
"Test_Acc": None,
"Final_Cost": None,
"Descending_Graph": True
}
r1, p1, c1 = runModels(h1, 40, True)
display(HTML(r1.to_html()))
*** Starting model training
*** Done!
| Epoch | HL_Units | HL_Size | Iterations | Learning_Rate | Lambda | Weight_Multi | Train_Acc | Test_Acc | Final_Cost | Descending_Graph | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 24 | 24 | 8 | 1 | 1150 | 0.009 | 0.9 | 0.0009 | 77.750 | 69.5 | 0.567576 | True |
| 9 | 9 | 5 | 1 | 1650 | 0.006 | 0.8 | 0.0006 | 71.875 | 68.0 | 0.510398 | True |
| 32 | 32 | 4 | 1 | 1500 | 0.007 | 1.7 | 0.0008 | 72.250 | 68.0 | 0.531841 | True |
| 36 | 36 | 8 | 1 | 1100 | 0.010 | 1.9 | 0.0008 | 78.125 | 68.0 | 0.595439 | True |
| 27 | 27 | 6 | 1 | 1650 | 0.010 | 1.2 | 0.0009 | 85.500 | 67.0 | 0.515924 | True |
| 12 | 12 | 4 | 1 | 1150 | 0.007 | 0.8 | 0.0001 | 73.625 | 66.5 | 0.608160 | True |
| 20 | 20 | 6 | 1 | 2000 | 0.006 | 1.1 | 0.0007 | 74.500 | 66.5 | 0.488919 | True |
| 21 | 21 | 4 | 1 | 800 | 0.009 | 0.2 | 0.0006 | 72.875 | 66.0 | 0.658947 | True |
| 1 | 1 | 3 | 1 | 1100 | 0.008 | 1.6 | 0.0005 | 70.000 | 65.5 | 0.564497 | True |
| 6 | 6 | 8 | 1 | 1250 | 0.006 | 0.5 | 0.0008 | 74.500 | 65.5 | 0.594659 | True |
| 13 | 13 | 3 | 1 | 1550 | 0.005 | 2.0 | 0.0002 | 73.250 | 65.5 | 0.592611 | True |
| 7 | 7 | 4 | 1 | 1500 | 0.010 | 1.3 | 0.0001 | 75.625 | 65.0 | 0.563984 | True |
| 10 | 10 | 8 | 1 | 1650 | 0.008 | 1.4 | 0.0008 | 82.000 | 64.5 | 0.552842 | True |
| 33 | 33 | 5 | 1 | 1950 | 0.005 | 1.5 | 0.0007 | 73.000 | 64.5 | 0.559365 | True |
| 0 | 0 | 7 | 1 | 850 | 0.007 | 1.6 | 0.0010 | 70.625 | 64.0 | 0.670679 | True |
| 5 | 5 | 6 | 1 | 1250 | 0.005 | 1.5 | 0.0003 | 69.750 | 64.0 | 0.647818 | True |
| 11 | 11 | 3 | 1 | 1800 | 0.010 | 1.1 | 0.0009 | 81.875 | 64.0 | 0.533753 | True |
| 16 | 16 | 6 | 1 | 1050 | 0.004 | 1.2 | 0.0007 | 65.250 | 64.0 | 0.665525 | True |
| 31 | 31 | 4 | 1 | 950 | 0.010 | 1.5 | 0.0008 | 74.375 | 64.0 | 0.642413 | True |
| 35 | 35 | 8 | 1 | 1150 | 0.006 | 2.0 | 0.0001 | 70.250 | 64.0 | 0.624042 | True |
| 39 | 39 | 7 | 1 | 2000 | 0.002 | 1.0 | 0.0003 | 62.875 | 64.0 | 0.670351 | True |
| 17 | 17 | 6 | 1 | 1500 | 0.004 | 0.9 | 0.0003 | 69.125 | 63.5 | 0.615967 | True |
| 18 | 18 | 7 | 1 | 1600 | 0.003 | 0.4 | 0.0005 | 66.500 | 63.5 | 0.651325 | True |
| 23 | 23 | 6 | 1 | 1700 | 0.003 | 1.3 | 0.0008 | 67.875 | 63.5 | 0.650475 | True |
| 37 | 37 | 3 | 1 | 950 | 0.005 | 1.4 | 0.0004 | 65.500 | 63.5 | 0.690524 | True |
| 15 | 15 | 5 | 1 | 1750 | 0.003 | 0.4 | 0.0002 | 66.500 | 62.5 | 0.667028 | True |
| 28 | 28 | 6 | 1 | 1550 | 0.003 | 1.8 | 0.0008 | 66.750 | 62.5 | 0.650610 | True |
| 4 | 4 | 6 | 1 | 1000 | 0.010 | 1.2 | 0.0007 | 75.250 | 61.5 | 0.513657 | True |
| 19 | 19 | 6 | 1 | 1250 | 0.003 | 0.6 | 0.0003 | 61.500 | 59.5 | 0.687296 | True |
| 25 | 25 | 6 | 1 | 1750 | 0.008 | 0.3 | 0.0003 | 63.750 | 59.5 | 0.472106 | True |
| 26 | 26 | 6 | 1 | 1850 | 0.008 | 1.3 | 0.0003 | 64.875 | 59.0 | 0.468910 | True |
| 3 | 3 | 5 | 1 | 900 | 0.004 | 1.2 | 0.0001 | 54.000 | 55.0 | 0.692530 | True |
| 8 | 8 | 7 | 1 | 800 | 0.004 | 0.5 | 0.0004 | 56.875 | 54.5 | 0.691068 | True |
| 38 | 38 | 8 | 1 | 1250 | 0.002 | 0.2 | 0.0010 | 53.250 | 54.5 | 0.689499 | True |
| 14 | 14 | 7 | 1 | 900 | 0.003 | 1.3 | 0.0010 | 55.875 | 54.0 | 0.691434 | True |
| 2 | 2 | 8 | 1 | 1050 | 0.001 | 1.7 | 0.0008 | 50.500 | 48.0 | 0.692637 | True |
| 22 | 22 | 5 | 1 | 1150 | 0.002 | 0.9 | 0.0008 | 51.250 | 48.0 | 0.690641 | True |
| 29 | 29 | 3 | 1 | 1450 | 0.001 | 0.1 | 0.0008 | 50.500 | 48.0 | 0.692755 | True |
| 30 | 30 | 7 | 1 | 900 | 0.001 | 1.2 | 0.0002 | 50.500 | 48.0 | 0.693133 | True |
| 34 | 34 | 5 | 1 | 1800 | 0.009 | 1.7 | 0.0003 | 84.750 | 65.5 | 0.625315 | False |
printCostGraphs(c1, list(r1.iloc[0:8, 0]), 4, (10,20))
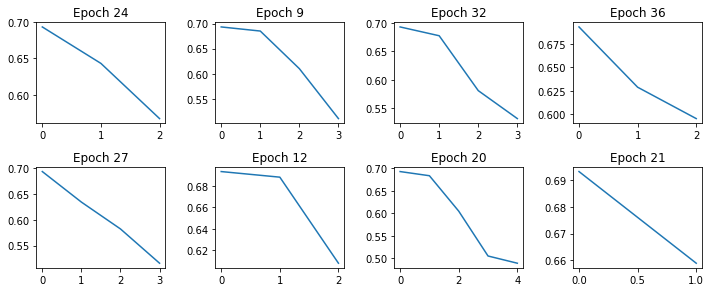
Smaller learning rate; more iterations
h3 = {
"Epoch": None,
"HL_Units": [2, 8, 1],
"HL_Size": 1,
"Iterations": [2000, 10000, 500],
"Learning_Rate": [0, .01, .001],
"Lambda": [0, 2, .1],
"Weight_Multi": [0, 0.001, .0001],
"Train_Acc": None,
"Test_Acc": None,
"Final_Cost": None,
"Descending_Graph": True
}
r3, p3, c3 = runModels(h3, 40, True)
display(HTML(r3.to_html()))
*** Starting model training
*** Done!
| Epoch | HL_Units | HL_Size | Iterations | Learning_Rate | Lambda | Weight_Multi | Train_Acc | Test_Acc | Final_Cost | Descending_Graph | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 36 | 36 | 7 | 1 | 3000 | 0.007 | 2.0 | 0.0002 | 90.250 | 70.0 | 0.349669 | True |
| 11 | 11 | 4 | 1 | 4500 | 0.005 | 0.7 | 0.0004 | 86.875 | 66.5 | 0.314388 | True |
| 39 | 39 | 8 | 1 | 3500 | 0.002 | 0.3 | 0.0006 | 72.625 | 66.5 | 0.564334 | True |
| 21 | 21 | 6 | 1 | 2500 | 0.003 | 0.9 | 0.0002 | 72.625 | 66.0 | 0.572031 | True |
| 37 | 37 | 8 | 1 | 3000 | 0.003 | 0.2 | 0.0001 | 77.250 | 66.0 | 0.521390 | True |
| 7 | 7 | 7 | 1 | 5500 | 0.005 | 1.2 | 0.0002 | 92.625 | 64.0 | 0.237177 | True |
| 8 | 8 | 4 | 1 | 2500 | 0.002 | 1.3 | 0.0001 | 65.000 | 64.0 | 0.664944 | True |
| 20 | 20 | 4 | 1 | 6500 | 0.005 | 0.6 | 0.0002 | 95.125 | 64.0 | 0.189869 | True |
| 17 | 17 | 7 | 1 | 5000 | 0.001 | 1.3 | 0.0010 | 67.625 | 63.5 | 0.626675 | True |
| 14 | 14 | 3 | 1 | 4000 | 0.001 | 0.2 | 0.0003 | 63.125 | 63.0 | 0.677799 | True |
| 25 | 25 | 4 | 1 | 3000 | 0.001 | 2.0 | 0.0001 | 50.625 | 48.0 | 0.690490 | True |
| 28 | 28 | 5 | 1 | 4000 | 0.008 | 1.0 | 0.0008 | 95.875 | 69.5 | 0.195421 | False |
| 0 | 0 | 4 | 1 | 5000 | 0.010 | 1.4 | 0.0003 | 97.625 | 68.5 | 0.151293 | False |
| 30 | 30 | 7 | 1 | 4500 | 0.008 | 0.6 | 0.0006 | 98.125 | 68.5 | 0.148196 | False |
| 35 | 35 | 4 | 1 | 3000 | 0.008 | 0.2 | 0.0006 | 89.000 | 68.5 | 0.535870 | False |
| 4 | 4 | 6 | 1 | 6000 | 0.009 | 1.0 | 0.0001 | 99.625 | 67.5 | 0.081284 | False |
| 5 | 5 | 8 | 1 | 5000 | 0.007 | 0.8 | 0.0002 | 96.000 | 67.5 | 0.176135 | False |
| 16 | 16 | 8 | 1 | 5000 | 0.010 | 1.4 | 0.0001 | 97.000 | 67.0 | 0.181041 | False |
| 19 | 19 | 6 | 1 | 9500 | 0.008 | 1.2 | 0.0002 | 100.000 | 66.5 | 0.047833 | False |
| 26 | 26 | 8 | 1 | 5500 | 0.009 | 0.1 | 0.0004 | 99.750 | 66.5 | 0.065625 | False |
| 31 | 31 | 7 | 1 | 10000 | 0.003 | 0.2 | 0.0008 | 99.125 | 66.5 | 0.101235 | False |
| 33 | 33 | 4 | 1 | 10000 | 0.009 | 1.2 | 0.0010 | 99.625 | 66.5 | 0.054953 | False |
| 34 | 34 | 7 | 1 | 8500 | 0.003 | 1.1 | 0.0006 | 97.250 | 66.0 | 0.156339 | False |
| 2 | 2 | 4 | 1 | 4000 | 0.007 | 1.0 | 0.0005 | 93.250 | 65.5 | 0.226588 | False |
| 6 | 6 | 7 | 1 | 10000 | 0.002 | 1.9 | 0.0007 | 91.500 | 65.5 | 0.243441 | False |
| 15 | 15 | 3 | 1 | 8500 | 0.002 | 0.1 | 0.0007 | 88.500 | 65.5 | 0.317150 | False |
| 24 | 24 | 7 | 1 | 6500 | 0.009 | 1.4 | 0.0009 | 99.750 | 65.5 | 0.070478 | False |
| 38 | 38 | 5 | 1 | 9000 | 0.004 | 1.6 | 0.0010 | 99.125 | 65.5 | 0.103912 | False |
| 3 | 3 | 7 | 1 | 4000 | 0.006 | 1.7 | 0.0010 | 90.125 | 65.0 | 0.248698 | False |
| 10 | 10 | 5 | 1 | 7500 | 0.008 | 0.6 | 0.0001 | 99.875 | 65.0 | 0.059867 | False |
| 12 | 12 | 4 | 1 | 8500 | 0.010 | 1.8 | 0.0010 | 97.625 | 65.0 | 0.160802 | False |
| 13 | 13 | 7 | 1 | 9000 | 0.009 | 0.1 | 0.0003 | 99.750 | 65.0 | 0.025635 | False |
| 18 | 18 | 6 | 1 | 9500 | 0.006 | 0.6 | 0.0001 | 100.000 | 65.0 | 0.046617 | False |
| 22 | 22 | 7 | 1 | 7000 | 0.003 | 0.4 | 0.0009 | 90.250 | 65.0 | 0.270268 | False |
| 23 | 23 | 3 | 1 | 7000 | 0.010 | 1.1 | 0.0001 | 89.125 | 64.5 | 0.233201 | False |
| 9 | 9 | 3 | 1 | 9000 | 0.006 | 0.6 | 0.0001 | 99.750 | 64.0 | 0.072092 | False |
| 32 | 32 | 7 | 1 | 8500 | 0.003 | 1.6 | 0.0005 | 96.250 | 64.0 | 0.169106 | False |
| 29 | 29 | 6 | 1 | 5000 | 0.003 | 0.1 | 0.0007 | 83.875 | 62.5 | 0.390400 | False |
| 1 | 1 | 7 | 1 | 8500 | 0.002 | 1.3 | 0.0002 | 88.000 | 61.0 | 0.320435 | False |
| 27 | 27 | 4 | 1 | 7000 | 0.007 | 0.5 | 0.0001 | 82.250 | 58.0 | 0.186820 | False |
printCostGraphs(c3, list(r3.iloc[0:8, 0]), 4, (10,20))
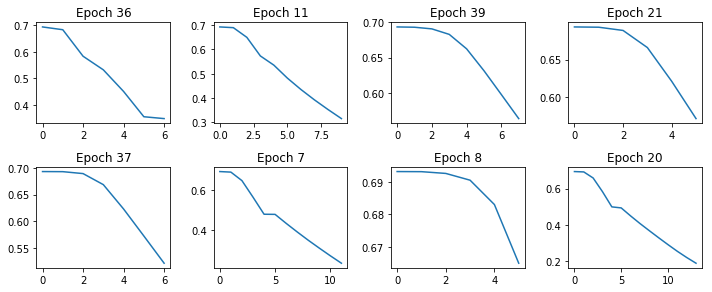
Larger learning rate training
h2 = {
"Epoch": None,
"HL_Units": [2, 8, 1],
"HL_Size": 1,
"Iterations": [750, 2000, 50],
"Learning_Rate": [0, .1, .01],
"Lambda": [0, 2, .1],
"Weight_Multi": [0, 0.001, .0001],
"Train_Acc": None,
"Test_Acc": None,
"Final_Cost": None,
"Descending_Graph": True
}
r2, p2, c2 = runModels(h2, 40, True)
display(HTML(r2.to_html()))
*** Starting model training
*** Done!
| Epoch | HL_Units | HL_Size | Iterations | Learning_Rate | Lambda | Weight_Multi | Train_Acc | Test_Acc | Final_Cost | Descending_Graph | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 6 | 1 | 1100 | 0.06 | 0.6 | 0.0002 | 83.375 | 73.0 | 0.350286 | True |
| 33 | 33 | 7 | 1 | 1450 | 0.06 | 1.8 | 0.0007 | 85.375 | 72.5 | 0.412003 | True |
| 3 | 3 | 8 | 1 | 1250 | 0.08 | 1.7 | 0.0007 | 82.625 | 71.0 | 0.478089 | True |
| 8 | 8 | 5 | 1 | 1200 | 0.06 | 1.5 | 0.0007 | 79.250 | 70.5 | 0.392045 | True |
| 15 | 15 | 7 | 1 | 1950 | 0.05 | 0.1 | 0.0010 | 90.500 | 70.5 | 0.311047 | True |
| 16 | 16 | 5 | 1 | 1800 | 0.06 | 0.3 | 0.0007 | 86.500 | 70.5 | 0.433791 | True |
| 27 | 27 | 5 | 1 | 900 | 0.07 | 1.5 | 0.0010 | 79.375 | 70.5 | 0.569526 | True |
| 36 | 36 | 8 | 1 | 1700 | 0.06 | 0.6 | 0.0005 | 91.000 | 70.5 | 0.327656 | True |
| 17 | 17 | 7 | 1 | 1350 | 0.05 | 2.0 | 0.0003 | 86.375 | 70.0 | 0.392760 | True |
| 19 | 19 | 3 | 1 | 1150 | 0.10 | 0.3 | 0.0007 | 82.000 | 69.5 | 0.447228 | True |
| 23 | 23 | 8 | 1 | 1900 | 0.10 | 0.2 | 0.0001 | 86.625 | 69.0 | 0.380536 | True |
| 24 | 24 | 7 | 1 | 1350 | 0.07 | 1.1 | 0.0010 | 85.750 | 69.0 | 0.426419 | True |
| 32 | 32 | 8 | 1 | 1000 | 0.01 | 0.6 | 0.0004 | 71.125 | 68.0 | 0.516636 | True |
| 2 | 2 | 7 | 1 | 1100 | 0.07 | 0.7 | 0.0002 | 87.125 | 67.5 | 0.505792 | True |
| 4 | 4 | 6 | 1 | 1850 | 0.09 | 0.7 | 0.0005 | 77.500 | 66.5 | 0.455560 | True |
| 28 | 28 | 5 | 1 | 850 | 0.03 | 1.5 | 0.0008 | 72.750 | 66.0 | 0.534921 | True |
| 6 | 6 | 6 | 1 | 1750 | 0.07 | 1.3 | 0.0004 | 71.000 | 65.0 | 0.375173 | True |
| 35 | 35 | 4 | 1 | 850 | 0.10 | 0.6 | 0.0002 | 69.750 | 63.5 | 0.585656 | True |
| 18 | 18 | 4 | 1 | 1050 | 0.05 | 0.4 | 0.0009 | 73.875 | 63.0 | 0.485734 | True |
| 26 | 26 | 5 | 1 | 1050 | 0.01 | 1.8 | 0.0009 | 62.625 | 61.0 | 0.523185 | True |
| 34 | 34 | 3 | 1 | 1750 | 0.01 | 0.6 | 0.0005 | 71.125 | 61.0 | 0.527912 | True |
| 5 | 5 | 7 | 1 | 1350 | 0.02 | 0.1 | 0.0004 | 66.375 | 60.0 | 0.435040 | True |
| 11 | 11 | 6 | 1 | 1800 | 0.06 | 1.2 | 0.0005 | 76.000 | 59.5 | 0.384182 | True |
| 37 | 37 | 3 | 1 | 1400 | 0.10 | 1.4 | 0.0002 | 58.875 | 59.5 | 0.495893 | True |
| 22 | 22 | 4 | 1 | 1600 | 0.10 | 1.1 | 0.0001 | 54.375 | 55.0 | 0.573383 | True |
| 31 | 31 | 6 | 1 | 1400 | 0.04 | 0.4 | 0.0007 | 86.875 | 74.0 | 0.550969 | False |
| 25 | 25 | 8 | 1 | 1050 | 0.03 | 0.4 | 0.0010 | 83.875 | 72.5 | 0.628924 | False |
| 29 | 29 | 7 | 1 | 1500 | 0.08 | 2.0 | 0.0003 | 80.375 | 72.5 | 0.447564 | False |
| 0 | 0 | 8 | 1 | 1550 | 0.03 | 1.2 | 0.0010 | 89.250 | 71.5 | 0.477405 | False |
| 9 | 9 | 4 | 1 | 1800 | 0.05 | 1.5 | 0.0005 | 89.375 | 71.0 | 0.349060 | False |
| 7 | 7 | 3 | 1 | 2000 | 0.07 | 0.3 | 0.0001 | 86.875 | 69.5 | 0.448897 | False |
| 21 | 21 | 3 | 1 | 1400 | 0.04 | 1.1 | 0.0010 | 86.750 | 69.0 | 0.564314 | False |
| 12 | 12 | 6 | 1 | 1500 | 0.08 | 1.9 | 0.0008 | 76.625 | 68.5 | 0.612455 | False |
| 39 | 39 | 4 | 1 | 1400 | 0.08 | 1.1 | 0.0001 | 75.500 | 68.0 | 0.578355 | False |
| 38 | 38 | 5 | 1 | 2000 | 0.04 | 1.6 | 0.0003 | 86.500 | 67.5 | 0.372239 | False |
| 10 | 10 | 7 | 1 | 1550 | 0.09 | 0.9 | 0.0007 | 86.875 | 66.0 | 0.422013 | False |
| 14 | 14 | 4 | 1 | 1750 | 0.07 | 1.9 | 0.0002 | 84.000 | 65.5 | 0.470529 | False |
| 13 | 13 | 3 | 1 | 1900 | 0.09 | 1.2 | 0.0007 | 67.250 | 62.0 | 0.455809 | False |
| 30 | 30 | 5 | 1 | 1450 | 0.06 | 1.8 | 0.0009 | 63.250 | 60.0 | 0.496687 | False |
| 20 | 20 | 4 | 1 | 1700 | 0.10 | 1.5 | 0.0010 | 65.750 | 59.0 | 0.600045 | False |
printCostGraphs(c2, list(r2.iloc[0:8, 0]), 4, (10,20))
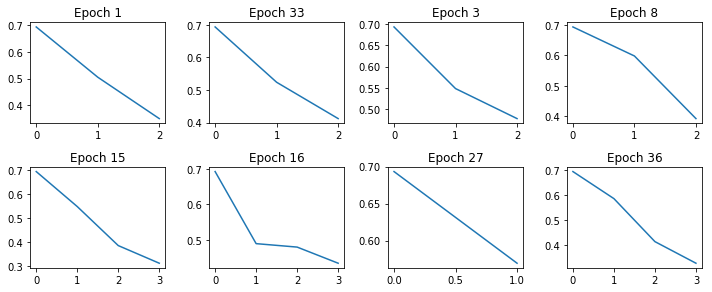
Larger learning rate; more iterations
h4 = {
"Epoch": None,
"HL_Units": [2, 8, 1],
"HL_Size": 1,
"Iterations": [2000, 10000, 500],
"Learning_Rate": [0, .1, .01],
"Lambda": [0, 2, .1],
"Weight_Multi": [0, 0.001, .0001],
"Train_Acc": None,
"Test_Acc": None,
"Final_Cost": None,
"Descending_Graph": True
}
r4, p4, c4 = runModels(h4, 40, True)
display(HTML(r4.to_html()))
*** Starting model training
*** Done!
| Epoch | HL_Units | HL_Size | Iterations | Learning_Rate | Lambda | Weight_Multi | Train_Acc | Test_Acc | Final_Cost | Descending_Graph | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 32 | 32 | 6 | 1 | 3000 | 0.02 | 1.6 | 0.0006 | 98.250 | 68.5 | 0.151224 | True |
| 6 | 6 | 4 | 1 | 2500 | 0.08 | 0.6 | 0.0003 | 79.500 | 67.0 | 0.402815 | True |
| 18 | 18 | 8 | 1 | 4500 | 0.08 | 0.6 | 0.0004 | 97.750 | 71.5 | 0.146351 | False |
| 38 | 38 | 7 | 1 | 3500 | 0.08 | 0.2 | 0.0009 | 85.750 | 70.5 | 0.410727 | False |
| 1 | 1 | 8 | 1 | 8500 | 0.09 | 1.8 | 0.0004 | 93.625 | 70.0 | 0.413673 | False |
| 24 | 24 | 3 | 1 | 5000 | 0.07 | 1.0 | 0.0003 | 96.875 | 69.5 | 0.193465 | False |
| 29 | 29 | 5 | 1 | 3000 | 0.03 | 0.8 | 0.0002 | 96.000 | 69.5 | 0.213647 | False |
| 33 | 33 | 6 | 1 | 9000 | 0.08 | 1.2 | 0.0002 | 95.250 | 69.5 | 0.237999 | False |
| 25 | 25 | 4 | 1 | 2500 | 0.03 | 1.5 | 0.0006 | 90.000 | 69.0 | 0.264472 | False |
| 26 | 26 | 3 | 1 | 6000 | 0.01 | 0.1 | 0.0003 | 95.875 | 69.0 | 0.238603 | False |
| 16 | 16 | 6 | 1 | 2500 | 0.08 | 1.5 | 0.0010 | 89.625 | 68.5 | 0.367724 | False |
| 39 | 39 | 5 | 1 | 10000 | 0.02 | 2.0 | 0.0002 | 98.500 | 68.5 | 0.127511 | False |
| 10 | 10 | 8 | 1 | 7000 | 0.09 | 1.9 | 0.0001 | 82.125 | 68.0 | 0.376518 | False |
| 19 | 19 | 6 | 1 | 10000 | 0.10 | 1.5 | 0.0007 | 88.000 | 68.0 | 0.465391 | False |
| 23 | 23 | 7 | 1 | 2500 | 0.09 | 1.9 | 0.0001 | 84.875 | 68.0 | 0.469647 | False |
| 35 | 35 | 4 | 1 | 2500 | 0.10 | 1.4 | 0.0001 | 86.250 | 68.0 | 0.342725 | False |
| 2 | 2 | 8 | 1 | 6000 | 0.03 | 1.3 | 0.0004 | 99.250 | 67.5 | 0.069514 | False |
| 5 | 5 | 4 | 1 | 3500 | 0.07 | 1.5 | 0.0002 | 81.375 | 67.0 | 0.603899 | False |
| 8 | 8 | 5 | 1 | 6500 | 0.03 | 0.2 | 0.0008 | 98.250 | 67.0 | 0.098654 | False |
| 28 | 28 | 6 | 1 | 8000 | 0.05 | 0.1 | 0.0003 | 96.000 | 66.5 | 0.175305 | False |
| 37 | 37 | 6 | 1 | 4000 | 0.07 | 0.8 | 0.0004 | 86.250 | 66.0 | 0.554717 | False |
| 9 | 9 | 6 | 1 | 8000 | 0.06 | 0.1 | 0.0006 | 98.125 | 65.0 | 0.075860 | False |
| 4 | 4 | 7 | 1 | 4500 | 0.10 | 1.9 | 0.0009 | 84.875 | 64.5 | 0.514395 | False |
| 14 | 14 | 3 | 1 | 6500 | 0.10 | 1.6 | 0.0002 | 82.000 | 64.5 | 0.460273 | False |
| 12 | 12 | 6 | 1 | 9000 | 0.02 | 0.4 | 0.0008 | 99.875 | 64.0 | 0.032819 | False |
| 30 | 30 | 7 | 1 | 10000 | 0.05 | 1.2 | 0.0006 | 87.750 | 64.0 | 0.369827 | False |
| 36 | 36 | 8 | 1 | 5000 | 0.03 | 1.6 | 0.0006 | 87.250 | 64.0 | 0.413589 | False |
| 34 | 34 | 4 | 1 | 5500 | 0.09 | 1.1 | 0.0005 | 80.125 | 62.0 | 0.415828 | False |
| 0 | 0 | 6 | 1 | 9000 | 0.05 | 0.6 | 0.0003 | 82.375 | 60.5 | 0.529366 | False |
| 13 | 13 | 4 | 1 | 3500 | 0.07 | 1.8 | 0.0002 | 75.000 | 60.5 | 0.481597 | False |
| 3 | 3 | 7 | 1 | 10000 | 0.07 | 0.7 | 0.0002 | 59.750 | 59.5 | 0.698914 | False |
| 31 | 31 | 7 | 1 | 9000 | 0.06 | 2.0 | 0.0005 | 79.375 | 59.0 | 0.538237 | False |
| 15 | 15 | 6 | 1 | 4000 | 0.07 | 1.6 | 0.0004 | 58.250 | 58.5 | 0.774961 | False |
| 11 | 11 | 6 | 1 | 7000 | 0.08 | 0.6 | 0.0002 | 70.250 | 58.0 | 0.627695 | False |
| 21 | 21 | 7 | 1 | 8000 | 0.08 | 1.0 | 0.0003 | 69.750 | 58.0 | 0.640571 | False |
| 7 | 7 | 5 | 1 | 8500 | 0.04 | 0.8 | 0.0006 | 56.250 | 55.5 | 0.662464 | False |
| 20 | 20 | 5 | 1 | 9500 | 0.10 | 0.1 | 0.0009 | 57.125 | 54.0 | 0.661862 | False |
| 17 | 17 | 8 | 1 | 10000 | 0.07 | 1.0 | 0.0009 | 52.875 | 53.5 | 0.553552 | False |
| 27 | 27 | 8 | 1 | 10000 | 0.08 | 1.2 | 0.0001 | 52.625 | 53.0 | 0.750212 | False |
| 22 | 22 | 4 | 1 | 6000 | 0.06 | 2.0 | 0.0003 | 54.000 | 49.5 | 0.885316 | False |
printCostGraphs(c4, list(r4.iloc[0:8, 0]), 4, (10,20))
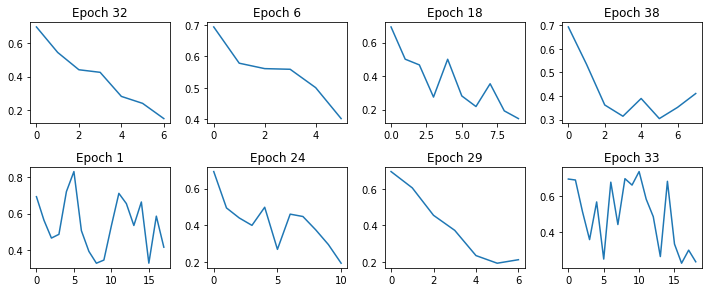
Verify Top Model
%%html
<style>
table {margin-left: 0 !important;}
</style>
If we examine the training results for the 160 models we find that the one with the best performance is the Epoch 1 model from the larger learning rate training batch.
It had the following hyperparameters:
| Hyperparameter | Value |
|---|---|
| Hidden Layer Units | 6 |
| Training Iterations | 1100 |
| Learning Rate: | 0.06 |
| L2 Lambda: | 0.6 |
| Weight Multiplier: | 0.0002 |
The test and training accuracy were:
| Dataset | Value |
|---|---|
| Train | 83.4% |
| Test | 73.0% |
Let’s train the model again, ensure we can reproduce the cost graph and test set accuracy rate, and then generate the F-Score for comparison.
Execute model with optimal hyperparameters
# Epoch HL_Units HL_Size Iterations Learning_Rate Lambda Weight_Multi Train_Acc Test_Acc Final_Cost Descending_Graph
# 1 6 1 1100 0.06 0.6 0.0002 83.375 73.0 0.350286 True
pLarge, cLarge, gLarge = model(trainingData, trainingLabels, 6, 1100, .06, .6, .0002, False, True)
trainingPredsLarge = predict(trainingData, pLarge, trainingLabels)
testPredsLarge = predict(testData, pLarge, testLabels)
print("\nTrain accuracy:", trainingPredsLarge["accuracy"])
print("Test accuracy:", testPredsLarge["accuracy"])
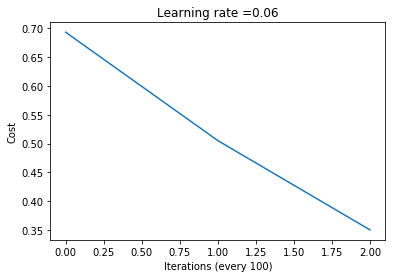
Train accuracy: 83.375
Test accuracy: 73.0
Generate F-Score
from sklearn.metrics import precision_recall_fscore_support as score
precision, recall, fscore, support = score(np.squeeze(testLabels), np.squeeze(testPredsLarge["predictions"]))
print('Precision: {}'.format(precision))
print('Recall: {}'.format(recall))
print('F-Score: {}'.format(fscore))
Precision: [0.69090909 0.77777778]
Recall: [0.79166667 0.67307692]
F-Score: [0.73786408 0.72164948]
Model Summary
So far in this series of write-ups we have the following results:
| Model Type | Test Set Accuracy | F-Score |
|---|---|---|
| Linear regression | 65.5% | [0.64974619 0.66009852] |
| Shallow neural network | 73.0% | [0.73786408 0.72164948] |
As we continue to explore other models and optimization we will hopefully see these metrics continue to improve.




Comments